Although the number pi (𝜋 = C/D) can be used for calculations, I do not use it as a circle constant. The mathematical constant pi (𝜋) is by definition only a calculation number, and nothing else. But a turn has a physical meaning, and it is also a circle property. Thus, a turn is the circle constant. Please, see my article Circle constant is a turn.

Circle constant is the turn value in radian:

      𝜃₀ = C/r ≈ 6.28 rad

 Here are two methods of squaring the circle. You can use the button F₁₁ for a full screen view.

The first method is based on the value 1 turn / 8 given by the Fig. 1a.

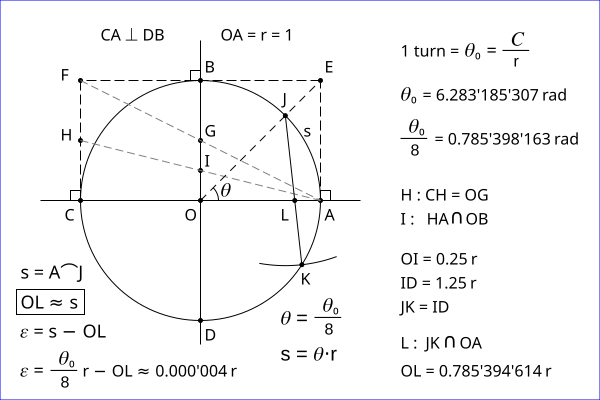
It is a simple method to find the arc length s of the angle 𝜃 = 1 turn / 8
(it is approximately the length OL). A turn is naturally the reference angle. Thus, the simple squaring the circle is given by the Fig. 1b.

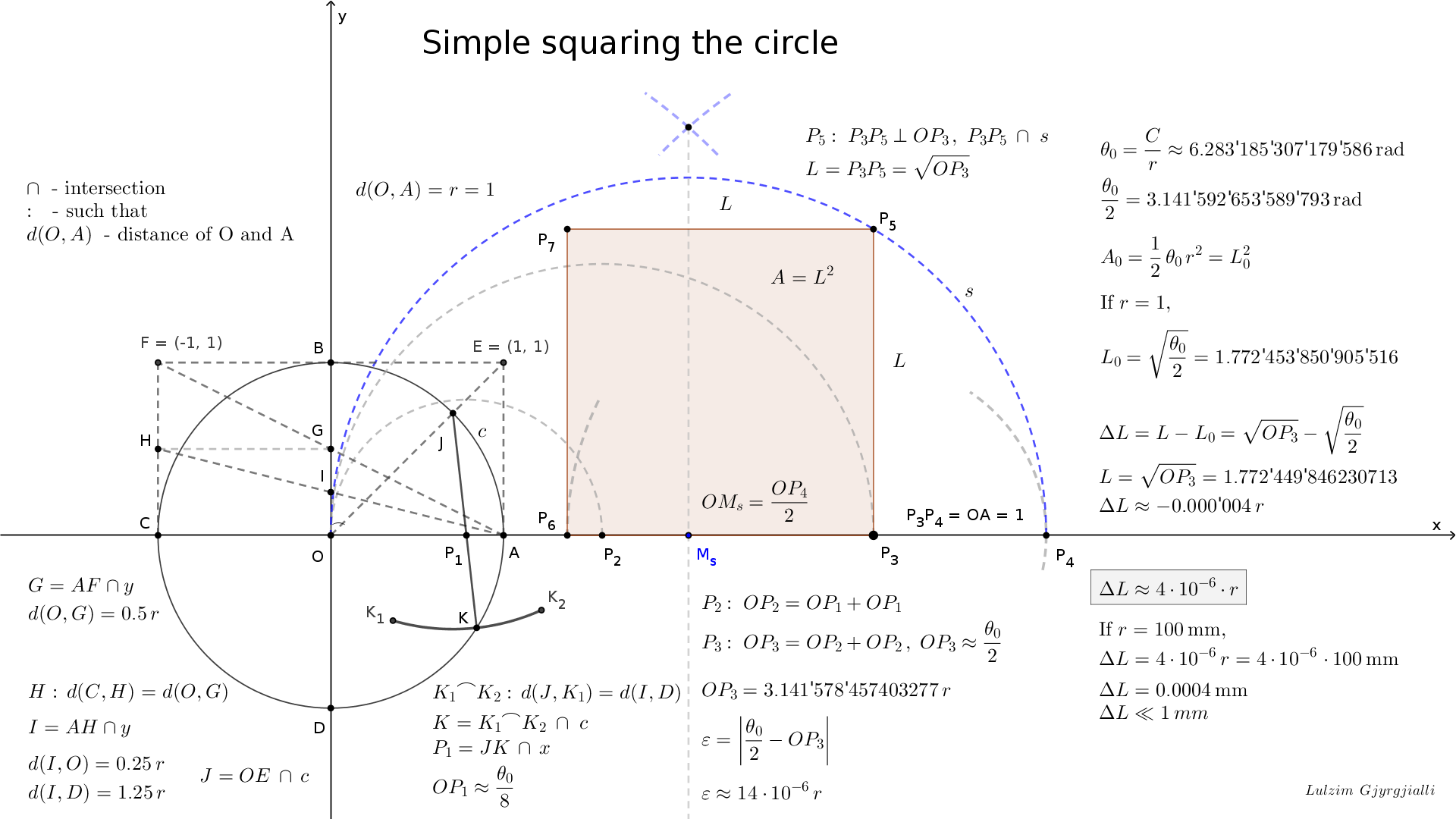
If the radius of the circle is r, and the side length of the square is L, the side length error of the square is ∆L ≈ 4 · 10^-6 r .
See simplestc.png .

The best accuracy you get by the method of the Fig. 2.

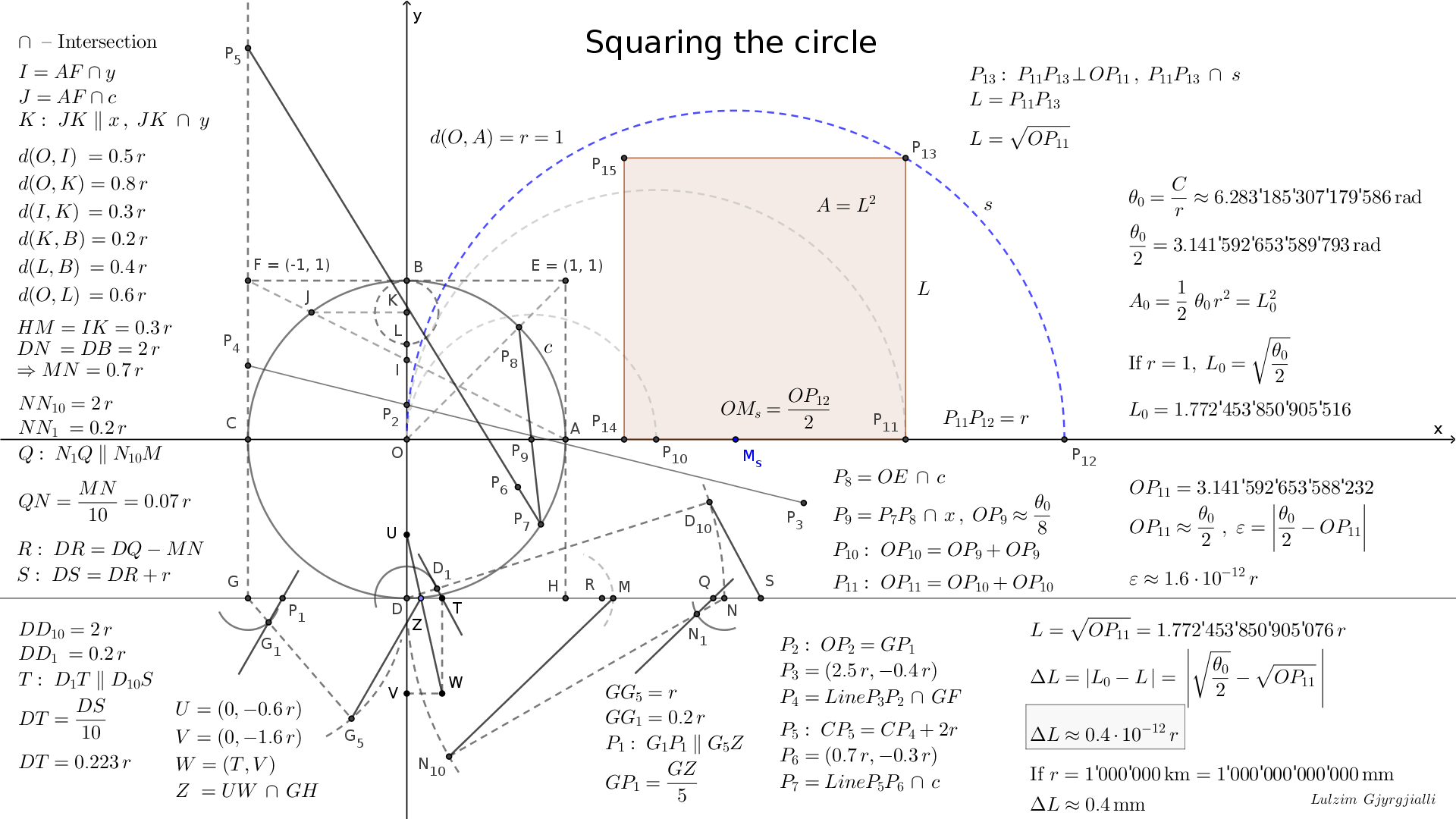
If the radius of the circle is r, and the side length of the square is L, the side length error of the square is ∆L ≈ 0.4 · 10^-12 r .
See squaringtc.png .

Note: 1'000'000 km ≈ 25 times around the earth (at the equator).