Golden ratio and the angle turn/10

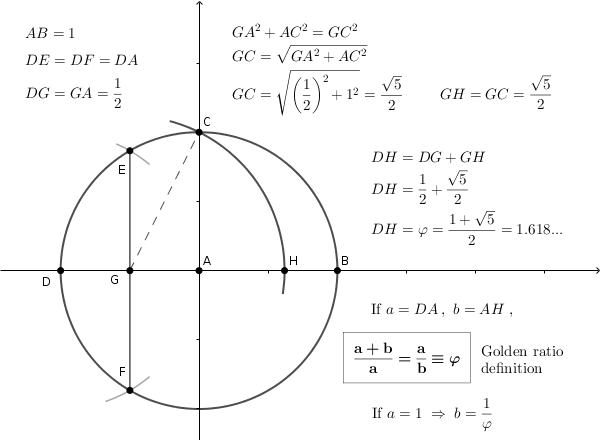
Let us have the golden ratio φ or phi (approx. 1.618). See the Fig 1 below.

The smaller version of the golden triangle has sides of length: a = 1 and b = 1/φ. See the image below.

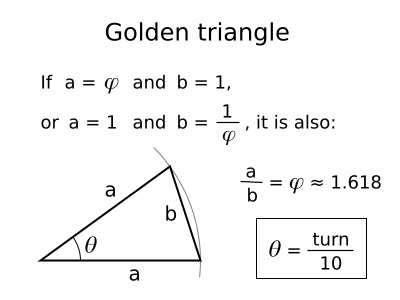
A turn represents a full rotation. The angle unit degree is defined by: 1° = turn/360. Thus, we get the value: 36° = turn/10 . I have a very simple method to draw the lengths φ, 1/φ and the angle turn/10. See the figure below.

Fig. 3 – Golden ratio and the angle turn/10.

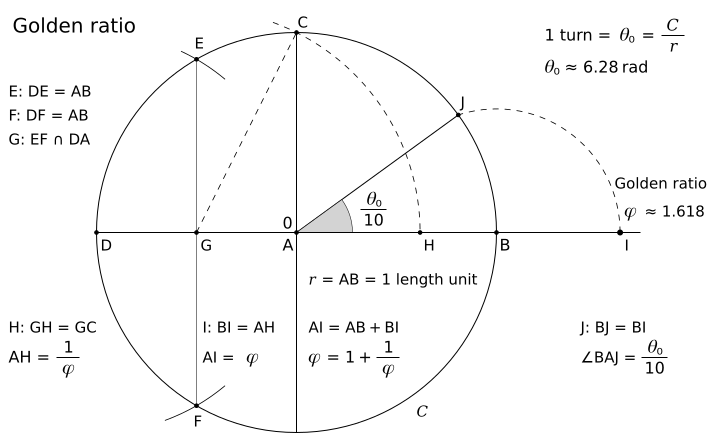
It is AB = AJ = 1 and BJ = BI = 1/φ . Thus, the triangle BAJ is a golden triangle. It must be emphasized that the angle of the golden triangle is ∠BAJ = turn/10. A turn is given by 1 turn = θ₀ = C/r, where C is the circumference of the circle, and r is the radius of the circle. Please, see the article Circle constant is a turn.

I am convinced that the method by a circle with the center in a point A and the points G: DG = GA and H: GH = GC in the figure above is the way how the golden ratio was invented. This is a logical reasoning. Probably many will not agree with me, but in my opinion:

The circle is one of the base elements of the geometry.

It can be used to represent a full rotation.You can describe a circle by the length coordinates

x² + y² = r²,

but it is only the line of a full rotation in a distance r. It is not easy to describe a rotation only by the length values.

Nature does not care for your definitions.
But, your definition must be in harmony with nature!

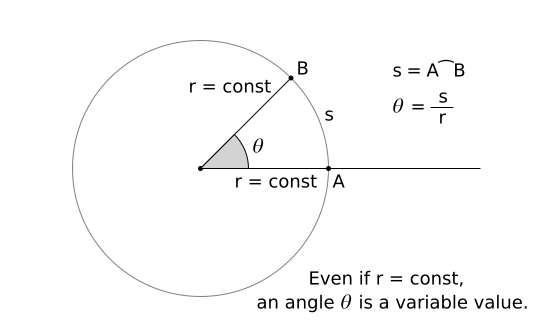
We can describe a position of a point on a circle by the arc length "s" relative to a start (initial) position "zero":

s = θ r

where r is the radius of a circle (it is a constant distance). If the circular motion is a movement along a circle, the distance of a movement is given by the arc length of the circle. But every angle is radius-invariant. It is like a movement along a straight line in one spacial dimension.

If x = constant, we get a "1-dimensional" ("straight") line in the x-y plane.
If r = constant, we get also a "1-dimensional" line in the θ-r plane! A circle represents a natural shape.

A circle is a "1-dimensional" line in the θ-r plane,
and it is like a straight line of a mathematical x-y plane!

A circle is given by a constant radius and the (always constant) full rotation. The points of a circular motion must be given by the angle values.

The length "r" is one physical dimension, and
the angle "θ" is the second physical dimension.

We get the angle turn/10 by the golden ratio of the two linear lengths! Think about it! And a circle is certainly used to invent the golden ratio as the ratio of the parts AH and HB of a circle radius AB! But, this method opens the way for the next article A better angle unit!

This work is licensed under the
Creative Commons Attribution 4.0 International License.
This is a Free Culture License!