A better angle unit

We have already the angle unit degree. It is defined by:

1° = turn/360

Is the definition of the unit degree the best definition we can have?

See also: Golden ratio and the angle turn/10
Go down to: Programming turn

An angle represents a rotation. It represents also a physical dimension. A physical unit must be easy to use. An angle is also a geometrical quantity.

The angle unit must be easy to construct!

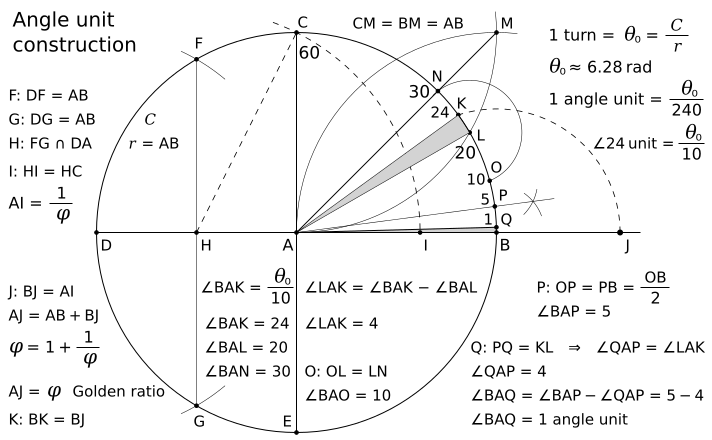
Can you construct an angle with the value 1° only by a compass and a straightedge? Nobody learns how to do it! There is always only the definition of the angle unit degree. But I know how to construct an angle with the value 1.5° only by a compass and a straightedge! If the angle 1.5° is easy to construct, it must be the angle unit. See first the angle values in the fig. 1 below.

Fig. 1 – Angles represented by the new angle unit turn/240.

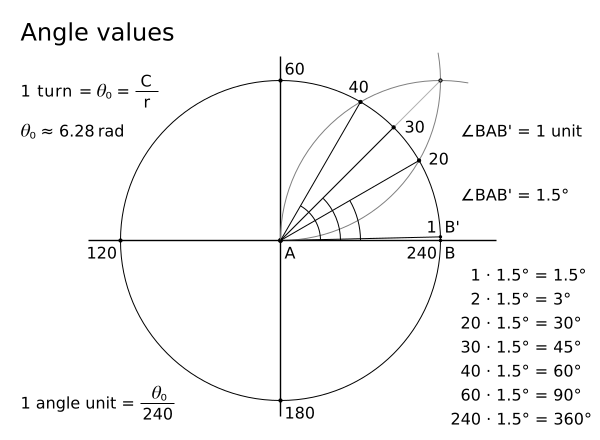
You can see that the right angle (90°) has 60 new angle units. All other angle values in the fig. 1 are easy to understand.

All my images have the accurate angles!

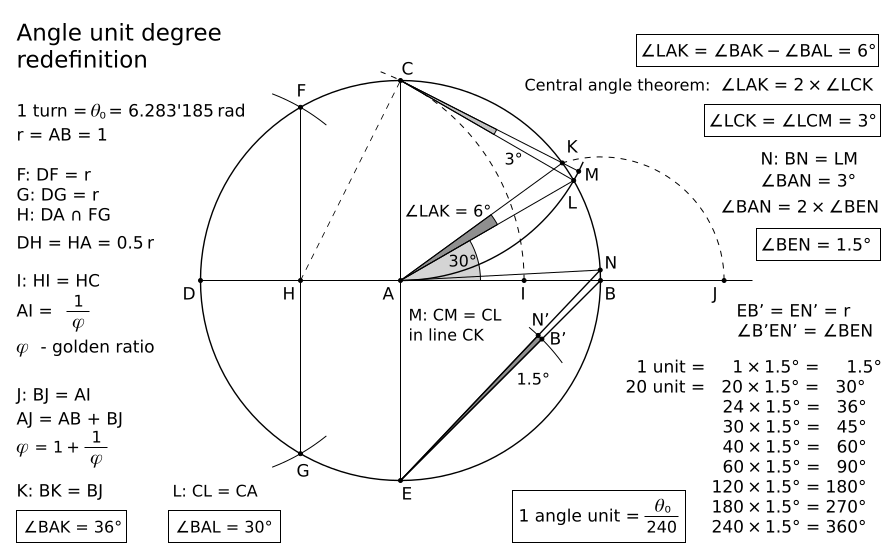
The angle unit degree defined by turn/360 is a very small unit. The angle unit turn/240 is also a very small unit, but it has a better size for a drawing. Any angle is as you know radius-invariant. If the circle radius is bigger, the arc of the angle unit is bigger. In this case we have a better visibility of the angle unit. You can zoom an image to see the difference. The construction of the angle unit turn/240 is given by the fig. 2 below.

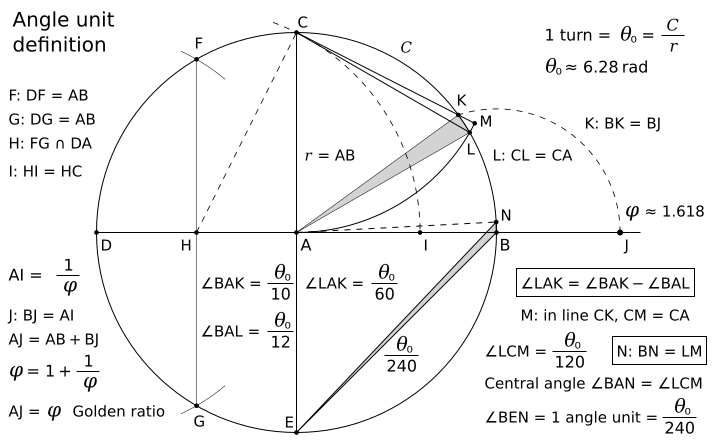
The angle unit degree is defined by turn/360. Thus, you can forget this image! We can define a new angle unit (equal to 1.5°) directly by a turn.

1 angle unit = 1.5° = turn/240

I have to use the unit degree for my explanations because the new angle unit turn/240 needs an acceptance. You can get the angle 36° = turn/10 by the golden ratio length 1/φ (the length BJ = AI in the image above), where φ is the golden ratio (approx. 1.618). The angle 30° = turn/12 is easy to construct. The difference angle 36° - 30° = 6° is also not a problem. Thus, the angle 6°/4 = 1.5° is easy to draw. Every subunit of a turn can be defined directly by a turn!

A turn is the natural reference angle.

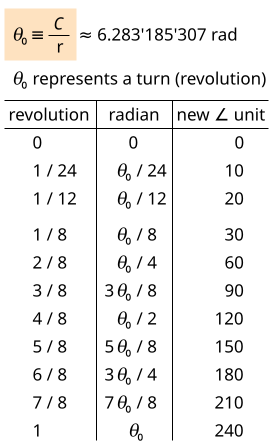
See the values below:

1 turn/10 = 36°

1 turn/12 = 30°

1 turn/60 = 6°

1 turn/240 = (1/4) · (1 turn/60)

1 turn/240 = 1.5°

A turn is also the circle constant (see: Circle constant is a turn). Thus, we can define the angle unit by a circle and a turn (1 turn = C/r).

Fig. 3 – Angle unit definition: 1 angle unit = turn/240.

Note:

89 ⁄ 55 ≈ 1.618... (approx. golden ratio)

This image (angle_unit_def.png) has the dimensions:
712px × 440px because 712px / 440px = (8 · 89px) / (8 · 55px) ≈ 1.618.
You can use the multiple values of the dimensions 89px and 55px to get approx. the golden ratio of an image:
(n · 89px) / (n · 55px) = 1.618...

This is like a classical construction! I have not a name for this new angle unit (1 turn/240)! But it has a reasonable definition! Keep it simple! You can see that the angle unit definition 1° = 1 turn/360 is not the best definition. We can have a better angle unit definition. See the values of the angular unit 1 turn/240:

The angle unit turn/240 is easy to use. This angle unit can be constructed also in the second way:

Fig. 5 – Construction of the angle unit turn/240 by the circle constant and the golden ratio (angle_unit_constr.png).

Thus, we can have the angle units: turn, radian and the unit 1 turn/240.

Fig. 6 – Angle unit and the circle constant 1 turn = C/r.

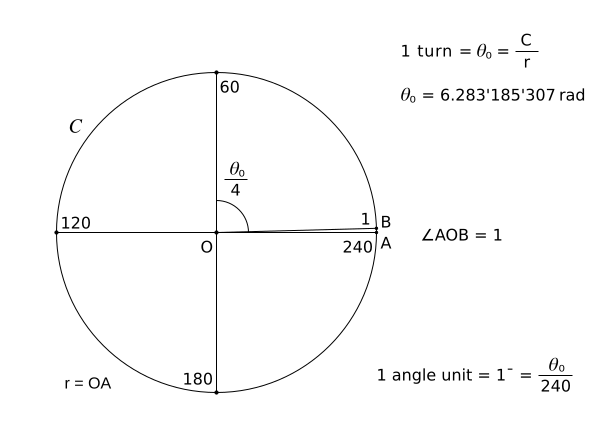
Yes! Circle constant is a turn in a circle:

Circle constant = 1 turn
Circle constant ≈ 6.283'185'307 rad
Circle constant = 360°
Circle constant = 240 new angle units

Circle constant is not only an abstract number. It has a concrete meaning! It represents a rotation. The magnitude of the turn in radian is the well known number (approx.) 6.283'185'307. This number is not a turn. A number can not be a turn. It is the magnitude of a turn in radian. But, even if you change the angle unit, a turn (full rotation) is always a turn. And it is still the circle constant! The abstractions are certainly very important. But, if math is the language of nature, do not forget nature in your math (geometrical) definitions. If we have the proper definitions, we know what we are talking about.

Fig. 7 – Shape angles by the new angle unit turn/240.

See a protractor with the angle unit turn/240 :

Fig. 8 – Protractor with the angle unit turn/240 (protractor.png).

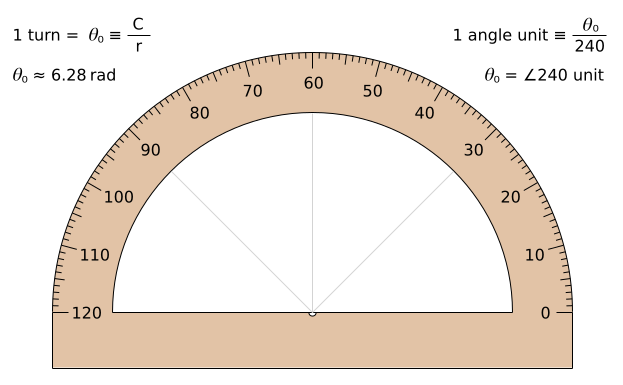
You can see less angle ticks on this protractor than on a protractor with our old angle degrees. Temporarily I am using the symbol overline ¯ (Unicode: U+00AF, or the decimal value ¯) for this new unit. The symbol of a measurement unit is very important. In this case, we need a new symbol! However, the new angle unit turn/240 can be called also "degree" (maybe with a notice that it is a "new degree") ! But, the others have to say also their opinion. Let us have the angles:

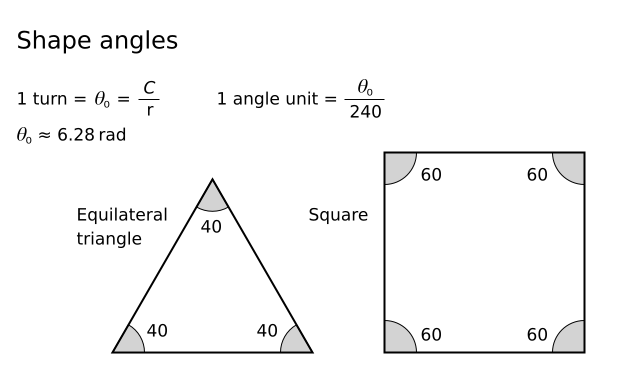
1·turn/8 + 2·turn/8 = 3·turn/8

If the angle unit degree is 1° = 1 turn/360, we get:

45° + 90° = 135°

But, if the angular unit is 1 turn/240, we get:

30 + 60 = 90 angle units.

See also the other multiple values of turn/8:

Fig. 10 – Angles given by the new angle unit turn/240.

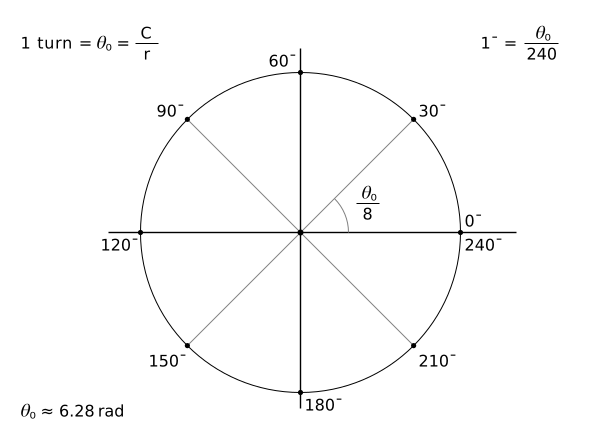
Simple sometimes means beautiful. Bisection of an angle is a division of the angle into two equal angles. As you know, it is not difficult to do it by a compass and a straightedge (ruler). Thus, let us see the half of the angle turn/8. If we use the angle unit degree, it is:

turn/16 = 360°/16 = 22.5°

We get a better result by: turn = 240 units

turn/16 = (240 units)/16 = 15 units

We get still an integer value. The number 360 has more divisors. But, who needs the divisor 9 or 18 of the number 360? There is no need to talk about the other divisors of the numbers 240 and 360! The number 360 is also a bigger number! If the world is divided into 24 time zones, every time zone can have 10 angle units turn/240 of longitude (much better than 15°). Do not forget that the unit turn/240 is also easy to construct only by a compass and a straightedge! The angle unit turn/240 is a better angle unit than our old angle unit degree defined by 1° = turn/360 !

If you say "angle unit definition", you have to say also the word "turn". A turn is always our natural reference angle.
We have to emphasize that the turn (a full rotation) is a "natural angle unit".

If you see turn = 240 unit, it is not the definition of turn. It is only a mathematical equality (needed for a calculation)! Also turn = 360° is not the definition of turn!

For the definition of a turn (full rotation) there is no need even for mathematics or any number! A turn is a physical constant, and it is very simple to define it. A turn is simply a full rotation around a position until you point in the same direction again.

A definition can give us a (new) meaning of something. And every equality is not a definition. Equalities are used for calculations. This is the reason why we have in this case two different symbols:

equality: symbol: = (U+003D EQUALS SIGN)
definition: symbol: ≡ (U+2261 IDENTICAL TO, ≡)

You may not define a turn by a subunit of a turn!
You may define an angle unit by a turn:
1 unit ≡ turn/240 (or 1° ≡ turn/360)

If we have the definition 1 angle unit ≡ turn/240, it is turn = 240 units.

The angle unit degree is also an angle, and it is a subunit of a turn. The first thing what a child learns is the rotation and the full rotation! In one direction is a parent, and in another direction is not! We already know what is a turn. Thus, the equality turn = 360° is not a definition! But, we have the definition of the unit degree: 1° ≡ turn/360.

We can define something new by something what we already know!

Forget the calculation number pi and the fraction pi/180. The calculation 1° = pi/180 is wholly unacceptable! The fraction pi/180 is only a calculation number and nothing else! It is not the definition of the angle unit degree!

An angle unit must be by definition an angle!

If the angle unit is a subunit of a turn, it is an angle. It represents also a rotation.

degree: - The basis for the definition of the angle unit degree is the constant angle turn. The unit degree is a subunit of a turn. It is good to give a direction, and it is good for orientation.
radian: - The basis for the definition of the angle unit radian is the fact that an angle is radius⁠-⁠invariant. The unit radian is an angle unit, but it is not (per definition) a subunit of a turn. It is good for mathematical calculations of the arc lengths.

If "s" is the arc length of a circle with a radius "r", the angle defined by 𝜃 (theta): 𝜃 = s/r is radius⁠-⁠invariant. If s = r, it is 𝜃 = 1 radian. In this case, a turn has approx. 6.28 rad. We have two different angle units degree and radian for two different views of the angle. But the turn is the natural unit!

Angle units:  deg (min=-240, max=240)

Angle: 0
Angle: 0

If you have a problem with this application, you need a browser with a better javascript support. You can get a better browser!

Programming turn

And here is something for the programmers. The Nim programming language is a new language for me. I have just started to test it (Nim Compiler Version 1.0.4, Compiled at 2019-11-27). It is easy to understand this language. The Nim code is like a pseudocode of a tutorial! But you can compile it! And the Nim programming language has its modules! See the code below:

#[ File: turn.nim Copyright (c) 2019-2020 Lulzim Gjyrgjialli. All rights reserved. Released under the MIT License See: turn_nim_license.txt ------------------------------ An angle represents a rotation. A turn represents a full rotation and it is always the reference angle. turn = 6.283185307179586 rad If the angle unit degree is defined by 1 deg = turn/240 it is 1 turn = 240 deg The trigonometric functions use only the radian values. Thus, we have to convert degrees to radians. ]# const turnRadians = 6.283185307179586 turnSubunits = 240.0 # Precalculated values RAD_OVER_DEG = turnRadians / turnSubunits DEG_OVER_RAD = turnSubunits / turnRadians type TurnValue = object rad*: float deg*: float const Turn* = TurnValue(rad: turnRadians, deg: turnSubunits) proc toRad*(degrees: float): float = return degrees * RAD_OVER_DEG proc toDeg*(radians: float): float = return radians * DEG_OVER_RAD

File: turn.nim
License: turn_nim_license.txt

I like the const section above (it declares the constants). The parts with "*" (U+002A ASTERISK, star) are visible outside of this module (file). If we decide to name the unit turn/240 by another name, we can make the procedure toDeg() obsolete, and we can define a new procedure for a new unit name (for example: toAngleUnit() or something else). Of course, in this case, also deg in Turn.deg must be changed. The implementation code (without a star symbol) in the module turn is not visible outside of this module. We can change it without a notice! You can save this code as a turn.nim file. This code can be tested by the code below:

# ------------------
# File: test.nim
# ------------------

import math # We need sin()
import turn # Turn, toDeg(), toRad()

echo "Turn.rad = ", Turn.rad, " rad"
echo "Turn.deg = ", Turn.deg, " deg"

var angle: float = 120
echo "120 deg = ", toRad(angle), " rad"

echo "Turn.rad / 4 has: ", toDeg(Turn.rad / 4), " deg"
echo "Right angle: sin(toRad(60)) = ", sin(toRad(60))

Save it as test.nim file and compile it. See: Nim
If you run it, you will see in a terminal:

Turn.rad = 6.283185307179586 rad
Turn.deg = 240.0 deg
120 deg = 3.141592653589793 rad
Turn.rad / 4 has: 60.0 deg
Right angle: sin(toRad(60)) = 1.0

This is my point of view: we need the elegant solutions! And the unit turn/240 is an "elegant" solution. However, it is a better angle unit!

This work is licensed under the
Creative Commons Attribution 4.0 International License.
This is a Free Culture License!